Miniaturized capacitors with carbon nanofibers

The world’s thin­nest dis­crete capa­cit­or has a total build­ing height is less than thirty micro­met­ers (30 µm). The capa­cit­or itself, without encap­su­la­tion, is a mere 0.5 to 10 µm. It can be built dir­ectly onto an integ­rated circuit’s die or built into its inter­poser. One square mil­li­meter has a capa­cit­ance of a whop­ping 650 nan­o­farads (650 nF/​mm2). Its intern­al res­ist­ance (ESR) is less than forty mil­liohms (40 mΩ), and its intern­al induct­ance (ESL) is below fif­teen pico­henry (15 pH).

Carbon nanofiber capacitors

We describe our capa­cit­or as a CNF-MIM capa­cit­or since it is a met­al-insu­lat­or-met­al (MIM) capa­cit­or where car­bon nan­ofibers (CNF) are used to cre­ate a much lar­ger sur­face area hence high­er capa­cit­ance than the form factor suggest.

Technical data

• Sol­id-state construction
• Capa­cit­ance dens­ity: > 650 nF/​mm²
• Equi­val­ent series res­ist­ance (ESR): < 40 mΩ
• Equi­val­ent series induct­ance (ESL): < 15 pH
• Break­down voltage: Up to ~ 25 V
• Leak­age cur­rent: ~ 4 mA/​F
• Excel­lent capa­cit­ance sta­bil­ity up to 150 °C

Applications for discrete CNF-MIM capacitors

A dis­crete CNF-MIM capa­cit­or has a smal­ler foot­print (area) and much thin­ner pro­file (z‑dimension) than any oth­er capa­cit­or with the same capa­cit­ance. CNF-MIM capa­cit­ors up to more than 650 nF can be made less than 30 µm in height. The actu­al form factor can be var­ied accord­ing to the design and need.

As shown in the illus­tra­tions, a dis­crete CNF-MIM capa­cit­or can be

• moun­ted on prin­ted cir­cuit board (PCB)
• embed­ded in PCB
• moun­ted on chip interposer
• embed­ded in chip interposer
• moun­ted on chip die

Dis­crete CNF-MIM capa­cit­ors are com­pat­ible with wafer to wafer (W2W) or die to wafer bond­ing (D2W).

Applications for integrated CNF-MIM capacitors

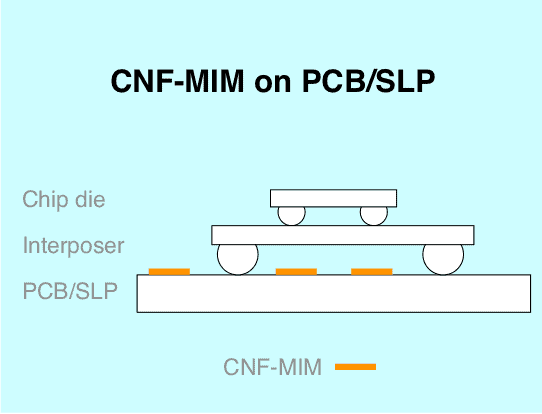
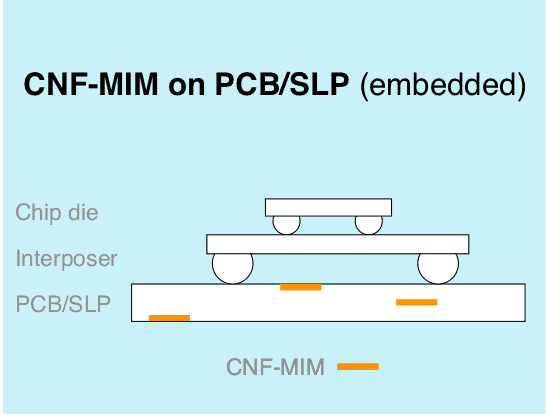
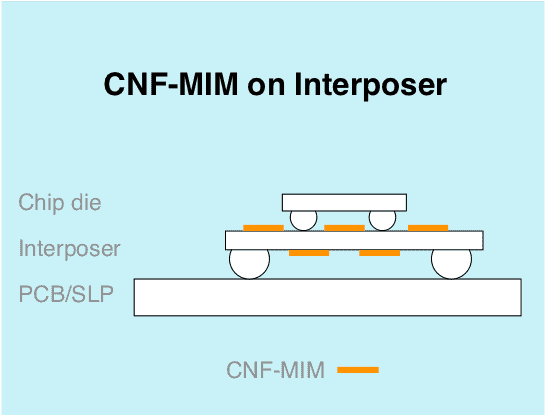
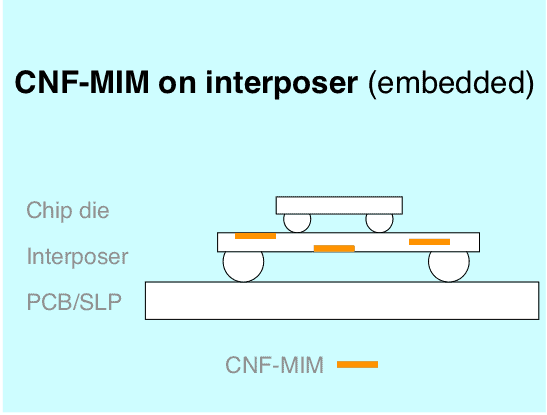
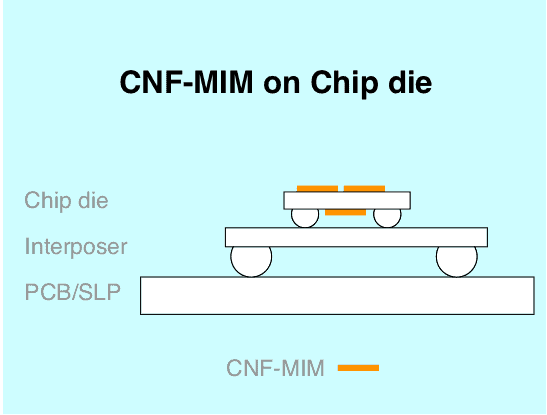
A CNF-MIM capa­cit­or can be integ­rated dir­ectly into chip die or chip inter­poser. The height of the integ­rated capa­cit­ors is a mere 0.5 to 10 µm. The bene­fits with integ­rated CNF-MIM are many:

• CMOS-com­pat­ible man­u­fac­tur­ing process
• Unpar­alleled design free­dom for cir­cuit designers
• Pos­sible to man­u­fac­ture dir­ectly on-chip
• Closer to the cir­cuit where it is needed
• Extremely small 2D footprint
• Very com­pact 3D volume
• Elim­in­ates the need for integ­rated dis­crete capacitors

As shown in the illus­tra­tions, a CNF-MIM capa­cit­or can be

• integ­rated with chip interposer
• integ­rated with built on-chip die

Discrete CNF-MIM capacitor compared to alternatives

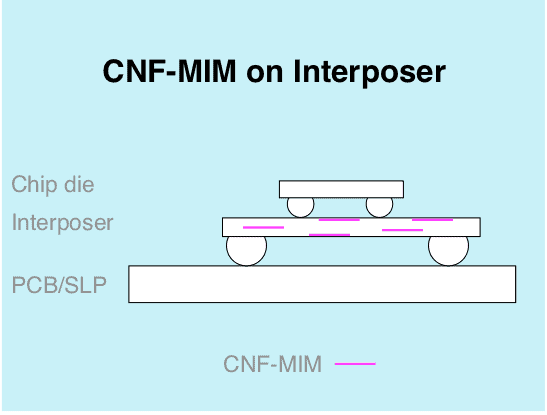
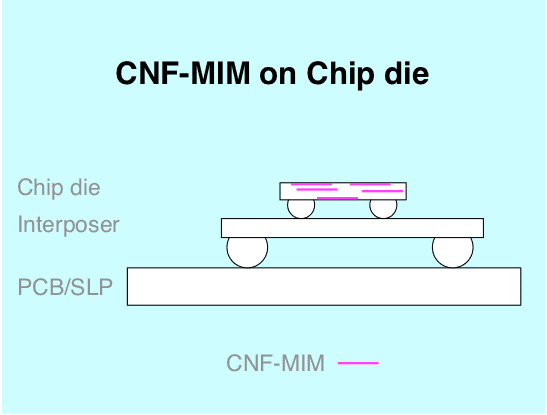
Mul­tilay­er Ceram­ic Capa­cit­ors (MLCC) form the industry stand­ard for sur­face-moun­ted device (SMD) capa­cit­ors. Every year, tril­lions of MLCCs are built into all kinds of elec­tron­ic devices. They are 300 µm high. CNF-MIM offers the same capa­cit­ance at a tenth of that height.

The mini­atur­iz­a­tion of elec­tron­ics is cre­at­ing a grow­ing need for ever smal­ler capa­cit­ors. And some cir­cuits (such as Apple’s) use capa­cit­ors that are state of the art. These use improve­ments of MLCC and Low Induct­ance Chip Capa­cit­ors (LICCs) and Trench Sil­ic­on Capa­cit­ors (TSCs), all of which have a height of 80–100 µm.

How­ever, MLCC, LICC, and TSC struggle to go down in height due to mater­i­als involved, pro­cessing schemes, and the cost of raw mater­i­als and pro­cessing. At the same time, SiP and SoC con­tin­ue to become more com­pact. There is less and less space between inter­con­nects (bumps), and they are get­ting short­er. To fit capa­cit­ors between the bumps, the capa­cit­ors must have a smal­ler foot­print and, above all, be shorter—preferably less than 20 µm.

This is the prob­lem that CNF-MIM capa­cit­ors solve. They have a much smal­ler foot­print and, above all, a much lower height.

How a MIM capacitor works

A met­al-insu­lat­or-met­al capa­cit­or, or MIM capa­cit­or for short, has par­al­lel met­al plates with a thin lay­er of an elec­tric insu­lat­or between them. The simplest form of a MIM-capa­cit­or is the par­al­lel plate capacitor.

Now, ima­gine we con­nect a bat­tery to a MIM-capa­cit­or. Since no cur­rent can pass through the isol­at­or, the elec­trons pushed into the plate on one side of the isol­at­or build up a pos­it­ive charge. The elec­trons pulled out from the plate on the oth­er side of the isol­at­or build a neg­at­ive charge. The charges increase respect­ively decrease the elec­tric­al poten­tial on the plates. The buildup con­tin­ues until the dif­fer­ence between the poten­tial is the same as the battery’s voltage. The dif­fer­ence in charge between the two plates cre­ates an elec­tric field between them.

When the bat­tery is removed, the elec­tric field remains since the charges have nowhere to go. Only when the capa­cit­or is con­nec­ted to a closed cir­cuit, the charges in the capa­cit­or can flow. The capa­cit­or thus stores energy in the form of an elec­tric field.

Any mater­i­al that does not con­duct cur­rent can be used as an elec­tric­al insu­lat­or. But gen­er­ally, dielec­tric mater­i­als are used.

Dielec­tric mater­i­al con­sists of atoms whose elec­trons can­not move freely enough to carry cur­rent like all insu­lat­ors. But unlike mater­i­als that are com­monly called insu­lat­ors, such as ceram­ics, dia­lectic mater­i­als become polar­ized in the pres­ence of an elec­tric field. They have elec­trons that are so free to move that the elec­tric field pulls them away from the nuc­le­us. Fig­ur­at­ively, the atom becomes elong­ated, with one end being neg­at­ively charged and the oth­er being pos­it­ively charged.

Dielec­tric in a MIM capa­cit­or becomes polar­ised when the elec­tric field is built up due to the plates’ dif­fer­ent charges. Because of the polar­iz­a­tion, the pos­it­ively charged plate comes into con­tact with the neg­at­ive ends of the atoms closest to it. That reduces its elec­tric­al poten­tial. The oppos­ite is hap­pen­ing at the neg­at­ively charged plate. The bat­tery responds by push­ing in even more charges to main­tain the elec­tric poten­tials. Since capa­cit­ance is a meas­ure of how much charge a capa­cit­or can store, the effect of using a dielec­tric is an increase in capacitance.

The ease with which a mater­i­al becomes polar­ized is pro­por­tion­al to its rel­at­ive per­mit­tiv­ity κ. The high­er the rel­at­ive per­mit­tiv­ity, the easi­er the mater­i­al becomes polar­ized. Thus, a dielec­tric with a high rel­at­ive per­mit­tiv­ity should be chosen to make a small capacitor.

How to make the worlds thinnest capacitor

To cre­ate a capa­cit­or with a min­im­al foot­print and height, we use car­bon nan­ofibers (CNFs) to mul­tiply the con­tact area between the two metals and the inter­me­di­ary dielectric.

Con­sider a single CNF with a dia­met­er of 10 nm and a length of 5 µm. Its mantle sur­face is 2,000 times lar­ger than the area it occu­pies.¹ Thus, a forest of such CNFs would mul­tiply the sur­face, but not by as much as 2,000. We can’t cov­er the entire ori­gin­al sur­face with CNFs; there must be space between them to allow access to the con­tact sur­face. But if the forest of CNFs cov­ers about half the sur­face, then the sur­face mul­ti­plic­a­tion would be in the range of 1,000 times.

CNF has many metal­lic prop­er­ties, includ­ing being a good con­duct­or of cur­rent. There­fore a met­al plate covered to fifty per­cent by CNFs is a single elec­trode with a sur­face area about 1,000 times lar­ger than the area of the met­al plate itself. By coat­ing this elec­trode with a uni­formly thick lay­er of a dielec­tric and then coat­ing this in turn with a met­al, a MIM capa­cit­or is obtained. Of course, the dielec­tric should have a high rel­at­ive per­mit­tiv­ity to max­im­ize the capacitance.

Since the CNF has a length much lar­ger than the dia­met­er, we can neg­lect what hap­pens to the elec­tric field near the base and top of each CNF. Essen­tially it will be a uni­form field, just as in a par­al­lel plate capacitor.

Since the capa­cit­ance of a par­al­lel plate capa­cit­or is dir­ectly pro­por­tion­al to the sur­face area, we con­clude that CNFs have increased the capa­cit­ance dens­ity by 1,000 times.

But it doesn’t end there. If the second lay­er of met­al is made uni­formly thick, both sides of it will have the same shape as the first elec­trode. So by coat­ing it with anoth­er lay­er of dielec­tric and then coat­ing this in turn with a met­al, anoth­er MIM capa­cit­or is obtained. It will have the same capa­city as the first. And by elec­tric­ally con­nect­ing the first and the third met­al lay­er, we achieve a par­al­lel con­nec­tion, which doubles the capa­cit­ance. This can be repeated as long as desired and there is space between the car­bon nan­ofibers. The last lay­er of met­al does not need to be uni­formly thick but can fill in any remain­ing spaces between the car­bon nanofibers.

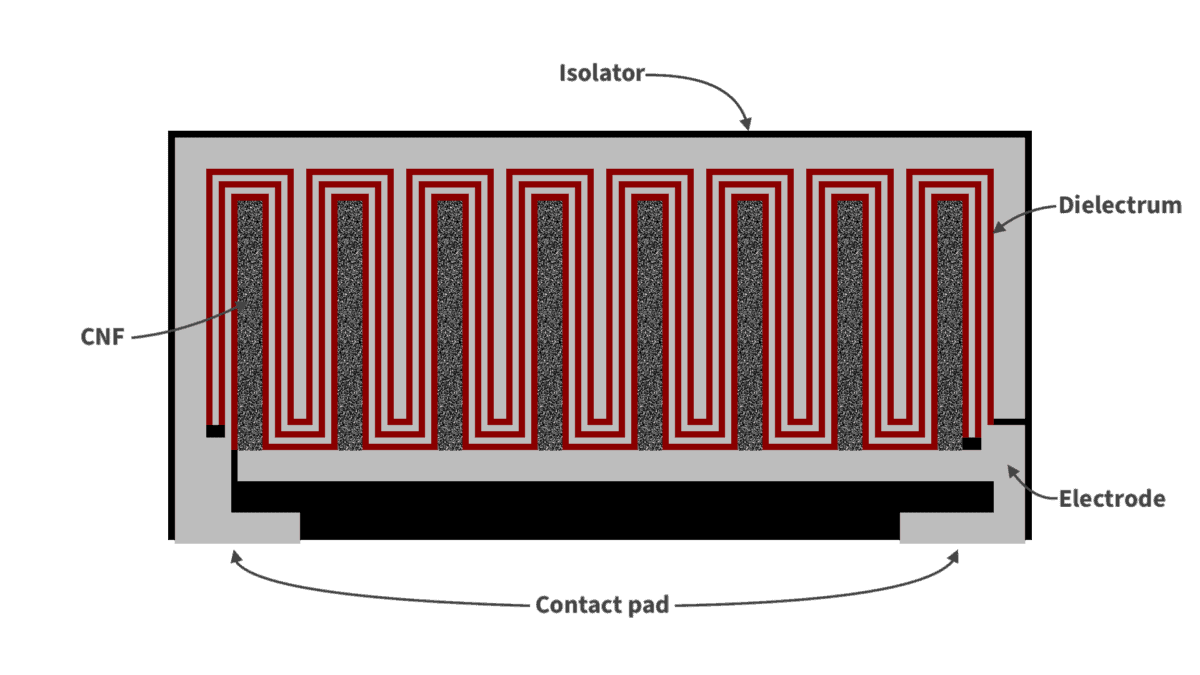
The fig­ure below shows a dis­crete CNF-MIM capa­cit­or with three CNF-shaped capa­cit­ors con­nec­ted in par­al­lel. Using the same assump­tions about dia­met­er, length, and dens­ity as above, this capa­cit­or has 3,000 times the capa­cit­ance pos­sible with a par­al­lel plate capa­cit­or in the same location.

1. Let r be the radi­us of the car­bon nan­ofiber, and h be its height. Then the ori­gin­al area A₁ = πr² and the new area A₂ = A₁ + 2πrh. The increase in area is A₂ /​ A₁ = (A₁ + 2πrh) /​ A₁ = 1 + 2πrh /​ (πr²) = 1 + 2h /​ r. If r = 5 nm and h = 5,000 nm, A₂ /​ A₁ = 1 + 2 ⋅ 5,000 /​ 5 = 2,001. ↩︎